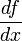مشتق
معزلی که فکر دانش اموزان زیادی را به خود معطوف داشته است. اینکه بتوان توسط فرمولهای مشتق محاسبات مشتقگیری از توابع را انجام داد ، مساله ی مهمی نبوده است. بلکه مفهوم مشتق و اینکه چه چیزی مشتق یک تابع است و همچنین از نظر نموداری مشتق چیست و مشتق پذیری چگونه بررسی میشود مورد نظر است.
به عنوان شخصی که سالها به طور تئوری درگیر این مساله بوده ام ، لازم میدانم که نکات زیر را به طور شهودی ، در حد توان فکری خودم ، بازگو کنم.
الف) مشتق یک تابع در نقطه ای مانند برابر است با شیب خط مماس در نقطه ی تماس ) (.
ب) از نظر مفهومی ، مشتق یک تابع در یک نقطه عبارت است از حد نسبت تغییرات تابع ( ) به تغییرات متغیر ( ) وقتی تغییرات متغیر خیلی کوچک شود (به سمت صفر میل کند) .
F ‘ (x ) = =
F ‘ (x ) = =
ج) اگر بخواهیم بدانیم یک تابع در یک نقطه مشتق پذیر است ، کافیست از روی نمودار بررسی کنیم که خط مماس بر منحنی در آن نقطه از طرف راست و از طرف چپ آن نقطه در یک امتداد باشند. (البته شیب این خط مماس نباید تعریف نشده باشد . به عبارت دیگر نباید بر محور x عمود باشد.)
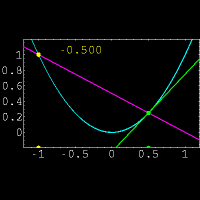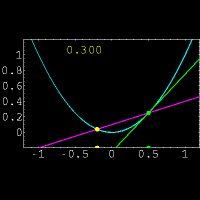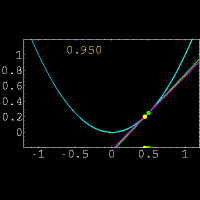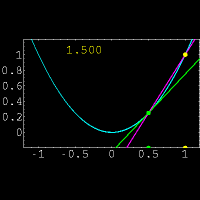
برای روشن تر شدن مطالب فوق توجهتان را به انیمیشن زیر جلب میکنم:

تذکر: secant line = خط قاطع ، tangent line = خط مماس ، slope = شیب
مشتق چیست؟
که این نحوهی نمایش را نمایش دیفرانسیلی مشتق مینامند.
تاریخچه:
مشتق از مسائل مهم ریاضی است که موضّع آن نیوتن و لایبنیتز بودند و حد مقدمه آن است. نیوتنسرعت لحظهای را به کمک قوانین حدگیری و لایبنیتز شیب خط مماس بر منحنیها را با استفاده از قوانین حدگیری محاسبه کرد، و هر یک در حالت کلی به مشتق رسید.
مشتقات مراتب بالاتر:
مشتقات مراتب بالاتر یک تابع از تعریف اصلی مشتق بدست میآیند. با مشتقگیری دوباره از مشتق یک تابع به مشتق دوم آن میرسیم و به همین ترتیب دیگر مشتقهای مراتب بالاتر نیز تعریف میشوند.
نحوهی نمایش:
مشتقات مراتب بالاتر (مشتق مرتبه دوم، سوم و چهارم) تابع f را میتوان به دو صورت زیر نمایش داد:
 و
و 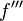 و
و 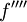
- f(۲) و f(۳) و f(۴)
تابع مشتقپذیر در یک نقطه:
اگر مشتق تابع  در نقطهای مانند
در نقطهای مانند  موجود و معین باشد، گفته میشود که تابع
موجود و معین باشد، گفته میشود که تابع  در نقطهی xمشتقپذیر است.
در نقطهی xمشتقپذیر است.
تابع مشتقپذیر:
اگر تابعی در هر نقطه از دامنهاش مشتقپذیر باشد، تابع مشتقپذیر نامیده میشود.
شرایط مشتقپذیری:
برای اینکه تابعی در یک نقطه مانند  مشتقپذیر باشد، باید در یک همسایگی آن تعریف شده باشد و نیز در آن نقطه پیوسته باشد. یا به عبارتی تابع در آن نقطه هموار باشد. البته این شرط لازم برای مشتق پذیری تابع در یک نقطه است.برای مثال در حالت های زیر تابع در نقطه a پیوسته است ولی مشتق پذیر نیست ۱نقطه بازگشتی مشتق بینهایت میشود ۲نقطه زاویه دار مشتق چپ و راست برابر نیست
مشتقپذیر باشد، باید در یک همسایگی آن تعریف شده باشد و نیز در آن نقطه پیوسته باشد. یا به عبارتی تابع در آن نقطه هموار باشد. البته این شرط لازم برای مشتق پذیری تابع در یک نقطه است.برای مثال در حالت های زیر تابع در نقطه a پیوسته است ولی مشتق پذیر نیست ۱نقطه بازگشتی مشتق بینهایت میشود ۲نقطه زاویه دار مشتق چپ و راست برابر نیست
مشتق تابع مرکب:
تابع ترکیب دو تابع 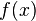 و
و 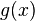 عبارت است از:
عبارت است از: 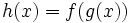 و مشتق این تابع مرکب عبارت است از:
و مشتق این تابع مرکب عبارت است از: 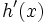
کاربردها:
پیدا کردن شیب خط:
پیدا کردن خطی که دریک نقطه بر یک منحنی مماس یا عمود است. برای معادله خط (y=f(x ، شیب خط قاطع برابر است با: m ، m=tanθ را شیب یا ضریب زاویهای میگویند. خطی که بر مماس بر منحنی عمود باشد، خط قائم بر منحنی مینامیم. بنابراین اگر m≠۰ شیب خط مماس و m شیب خط قائم بر منحنی باشد، آنگاه داریم: m.m= -۱
از مشتق میتوان در ساختن جامدادی ، وسایل نظامی ، در ساختن قطب نما و غیره استفاده کرد یعنی میتوان با استفاده از مشتق شیب مثلاً جامدادی را محاسبه کنیم. مثلاً در ساختن دیدبانی میتوان از ضریب زاویهای استفاده کرد. در صورتی که شیب در نقطه n مساوی صفر باشد آنگاه مماس بر منحنی در این نقطه، خطی افقی یا موازی محور x است. بنابراین خط قائم بر منحنی در این نقطه، خطی عمودی یا موازی محور y خواهد بد و داریم: ∞ = (m(a
محاسبه تغیرات یک کمیت نسبت به دیگری:
با استفاده از مشتق میتوان مقدار تغییرات یک کمیت را نسبت به کمیت معین دیگری، وقتی این دو کمیت به وسیله تابعی به هم مربوط هستند، به دست آورد. مثلاً اگر (g(r مساحت دایرهای به شعاع r باشد، داریم: g(r) = π r۲ آنگاه مقدار لحظهای تغییر مساخت دایره نسبت به شعاع آن برابر است با g(r) = ۲πr مقدار لحظهای تغییر مساحت این دایره، وقتی شعاع آن برابر مقداری مثل r=۱ باشد، برابر است با: g(۱) = ۲π
پیدا کردن شتاب:
اگر (S(t معادله حرکت جسم متحرک باشد آنگاه V را متوسط سرعت در یک فاصله زمانی میگویند. اگر از سرعت متوسط مشتق بگیریم مقدار شتاب حرکت بدست میآید. که شتاب را با (a(t نشان میدهند یعنی شتاب در لحظه t میباشد. (a(t)=V(t)=S"(t
محاسبه انرژی جنبشی:
میدانیم انرژی جنبشی جسمی به جرم m و سرعت V عبارت است از ۲/(m.v^۲) برای بدست آوردن انرژی جنبشی میتوان سرعت را از طریق گرفتن مشتق از معادله حرکت بدست آورد سپس مقدار V را در معادله انرژی جنبشی قرار داد.
پیدا کردن ماکزیمم و مینیمم نسبی توابع:
اگر تابعی در یک نقطه از یک بازه اکسترمم نسبی داشته باشد و مشتق تابع نیز در آن نقطه وجود داشته باشد آنگاه مشتق تابع در آن نقطه مساوی صفر است. منظور از اکسترمم نسبی داشتن ماکزیمم یا مینیمم نسبی در یک نقطه است. ماکزیمم نسبی و مینیمم نسبی به صورت زیر تعریف میشوند:
تابع f در نقطه d یک "ماکزیمم نسبی" دارد هر گاه (f(d)≥f(x تابع f در نقطه C یک "مینیمم نسبی" دارد هر گاه (f(c)≤f(x
پیدا کردن تابع صعودی و نزولی:
اگر برای همه مقادیر (xε(a,b داشته باشیم:
اگر مشتق f بزرگتر از صفر باشد آنگاه f تابعی صعودی است. اگر مشتق f کوچکتر از صفر باشد آنگاه f تابعی نزولی است.
تعیین نقاط بحرانی توابع:
نقطه C از قلمرو f را یک نقطه بحرانی f مینامیم، در صورتی که یکی از دو شرط زیر برقرار باشد: ۱- مشتق f در نقطه c وجود نداشته باشد. ۲- مشتق f در نقطه C مساوی صفر باشد.
فرض کنید C یک نقطه بحرانی تابع f(c)=۰,f باشد، داریم:
اگر مشتق مرتبه دوم f در نقطه C کوچکتر از صفر باشد، آنگاه f در نقطه C ماکزیمم نسبی دارد.
اگر مشتق مرتبه دوم f در نقطه C بزرگتر از صفر باشد، آنگاه f در نقطه C مینیمم نسبی دارد.
پیدا کردن تقعر، تحدب و نقطه عطف:
منحنی (y = f(x را در نقطه ( (C , f(C ) مقعر مینامیم، اگر مشتق در نقطه C وجود داشته باشد و برای هر x متعلق به این بازه در بالای خط مماس بر منحنی واقع باشد. منحنی (y=f(x را در نقطه ( (C , f(C ) محدب مینامیم، اگر مشتق f در نقطه C وجود داشته باشد برای هر x متعلق این بازه در پایین خط مماس بر منحنی واقع باشد.
یا داشته باشیم:
اگر مشتق مرتبه دوم f در نقطه C بزرگتر از صفر باشد، آنگاه منحنی f در نقطه c مقعر است.
اگر مشتق مرتبه دوم f در نقطه c کوچکتر از صفر باشد، آنگاه منحنی در نقطه C محدب است.
نقطه عطف: اگر روی یک منحنی نقطهای وجود داشته باشد که در آن نقطه تقعر منحنی بر تحدب تغییر کند یا بر عکس، آن را یک نقطه عطف مینامیم. یا میتوانیم بگوییم: f"(C) = ۰
| d dx |
sin x | = cos x |
مشتق تابع کسینوس برابر است با:
|
مشتق تابع تانژانت برابر است با:
| d dx |
tan x = sec²x |
مشتق تابع کتانژانت برابر است با:
| d dx |
cot x = −csc²x |
مشتق تابع سکانت برابر است با:
| d dx |
sec x | = sec x tan x |
مشتق تابع کسکانت برابر است با:
| d dx |
csc x | = | −csc x cot x |
- ۹۴/۱۰/۰۱