تابع چگالی احتمال

در آمار و احتمالات تابع چگالی احتمال به تابعی اطلاق می‌شود که توزیعی آماری را به شکل انتگرالی نمایش دهد. مقدار این تابع غیر منفی است.

توزیع پیوسته یک متغیره

 

تابع توزیع نرمال N(0, σ²).

اعداد استر لینگ

در ریاضیات ٬ در بسیاری از مسائل آنالیز ریاضی و ترکیبیات به اعداد استرلینگ برمی‌خوریم.این اعداد به نام جیمز استرلینگ نام‌گذاری شده‌اند.

تکینک های انتگرال گیری

تکنیکهای انتگرال گیری- روش انتگرال گیری جزء به جزء

 

اگر u و v  توابعی از  x باشند قاعده مشتق حاصلضرب می گوید

 

 با انتگرال گیری از طرفین داریم

 

 

 

انتگرال

 

نمایش گرافیکی انتگرال.

اَنتِگرال (به انگلیسی: Integral) مقدار مشترک ممکن زیرینۀ مجموعه‌ای ریمانی و زبرینۀ مجموعه‌ای ریمانی یک تابع حقیقی در بازۀ مفروض است.^[۱] انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل می‌دهند.

نخستین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد.

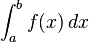
 و  نقاط ابتدا و انتهای بازه هستند و  تابعی انتگرال‌پذیر است و 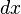 نمادی برای متغیر انتگرال‌گیری است.

از لحاظ تاریخی 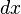 یک کمیت بی‌نهایت کوچک را نشان می‌دهد. هر چند در تئوری‌های جدید، انتگرال‌گیری بر پایه متفاوتی پایه‌گذاری شده‌است.

لیمیت ( حد )

وقتی که مقادیر متوالی به یک متغیر نسبت داده می‌شود، و آن متغیر بی‌نهایت به عدد ثابتی نزدیک شود، به طوری که اختلاف آنها از مقدار ثابت به هر اندازه کوچک قابل انتخاب باشد، این مقدار ثابت را حد همه مقادیر متغیر می‌گویند.

کاربرد مفهوم حد در ریاضی در توصیف مقداری است که یک تابع یا دنباله به آن نزدیک می‌شود، هنگامی که ورودی آن تابع یا شمارندهٔ آن دنباله به یک مقدار مشخص نزدیک می‌شود.^[۱] حد یک مفهوم اساسی در حساب دیفرانسیل و انتگرال و در حالت کلی در آنالیز ریاضی است و در تعریف پیوستگی، مشتق و انتگرال کاربرد دارد. موضوع حد، به منظور بیان رفتار یک تابع می‌پردازد و می‌تواند رفتار آن را در نقاط روی صفحه و یا در بی نهایت هم ارزیابی کند.

مفهوم حد یک دنباله به حالت کلی تر حد شبکهٔ مکان‌شناسی گسترش می‌یابد و ارتباط نزدیکی با حد و حد مستقیم در نظریهٔ رده‌ها دارد.

ریاضی‌دانان پیش از آنکه مفهوم دقیق تر حد را ارائه کنند، در مورد آن مجادله‌های بسیار کرده‌اند. یونانی‌ها در عصر باستان درکی از مفهوم حد داشته‌اند. برای نمونه ارشمیدس مقدار تقریبی را با استفاده از پیرامون چند ضلعی‌های منتظم محاط در دایره به شعاع یک، وقتی که تعداد اضلاع بدون کران افزایش می‌یابد به دست می‌آورد. در قرون وسطی نیز تا دورهٔ رنسانس مفهوم حد برای بدست آوردن مساحت شکل‌های گوناگون بکار گرفته می‌شد.^[۲]

در نوشتار ریاضی حد را گاهی به صورت lim نمایش می‌دهند مانند lim(a_n) = a، گاهی با یک پیکان رو به راست (→) نمایش می‌دهند مانند: a_n → a و گاهی هم به فارسی حد می‌نویسند.

مشتق

معزلی که فکر دانش اموزان زیادی را به خود معطوف داشته است. اینکه بتوان توسط فرمولهای مشتق محاسبات مشتقگیری از توابع را انجام داد ، مساله ی مهمی نبوده است. بلکه مفهوم مشتق و اینکه چه چیزی مشتق یک تابع است و همچنین از نظر نموداری مشتق چیست و مشتق پذیری چگونه بررسی میشود مورد نظر است.

به عنوان شخصی که سالها به طور تئوری درگیر این مساله بوده ام ، لازم میدانم که نکات زیر را به طور شهودی ،  در حد توان فکری خودم ، بازگو کنم.

حل مسائل پیچیده ریاضی با سفر کامپیوتری در زمان

یک تیم بین‌المللی از دانشمندان در تحقیقات جدید خود نشان داده‌اند که کامپیوترهای کوانتومی در آینده می‌توانند مسائل لاینحل ریاضی را با ارسال داده‌ها به زمان عقب حل کنند.

 

به گزارش بیگ بنگ به نقل از ایسنا، به گفته محققان، مدل کامپیوتر کوانتومی که در زمان سفر می‌کند، اطلاعاتی را تولید می‌کند که می‌توان آن را با فیزیک کوانتومی به منحنی زمانی بسته ارسال کرد. اینها، مسیرهایی از میان بافت فضا-‌زمان هستند که به خودشان برمی‌گردند. نسبیت عام اجازه می‌دهد چنین مسیرهایی در پیچیدگی فضا-زمان موسوم به کرم‌چاله‌ها وجود داشته باشند.

23 مسئله هیلبرت

در سال ۱۹۰۰ میلادی دیوید هیلبرت (۱۸۶۲- ۱۹۴۳م) در دومین کنگره بین المللی ریاضی دانان در پاریس در یک سخنرانی از مسائل ریاضیات سخن گفت و پس از آن هرمن ویل (Herman Weyl) درباره آن مسائل چنین گفت: «هرکس این مسائل را حل کند به کلاس افتخاری ریاضیدانان وارد می شود.» در همین سال هیلبرت به یک ریاضیدان برجسته در آلمان تبدیل شد.

معادله کپلر

download

حل مسئله ریمان پس از 156 سال !

استادی نیجریایی ادعا می‌کند موفق به حل معمایی شده که بیش از ۱۵۰ سال ذهن دانشمندان و ریاضیدانان جهان را به خود مشغول کرده‌است و یکی از هفت مساله لاینحل دانش ریاضیات به شمار می‌رود.