وبلاگ علمی دنفر

ریاضیات و فیزیک ، جهانی جدا

وبلاگ علمی دنفر

ریاضیات و فیزیک ، جهانی جدا

وبلاگ علمی دنفر

وارد علـم شو ،
تا از مـا شوی !

طبقه بندی موضوعی
کلمات کلیدی

انرژی هسته ای

جان نش

بایگانی
آخرین مطالب
پیوندها
پیوندهای روزانه
ساخت وبلاگ در بلاگ بیان، رسانه متخصصان و اهل قلم

اعداد استر لینگ

يكشنبه, ۶ دی ۱۳۹۴، ۱۲:۵۷ ب.ظ

در ریاضیات ٬ در بسیاری از مسائل آنالیز ریاضی و ترکیبیات به اعداد استرلینگ برمی‌خوریم.این اعداد به نام جیمز استرلینگ نام‌گذاری شده‌اند.

نمایش عدد استرلینگ نوع اول

عدد استرلینگ نوع اول را بدون در نظر گرفتن علامت به شکل زیر نشان می‌دهند.

s(n,k)

ودر حالت عادی (با در نظر گرفتن علامت) عدد به صورت زیر نمایش داده می شود.

c(n,k)=\left[{n \atop k}\right]=|s(n,k)|

عدد استرلینگ نوع اول

c(n,k)=\left[{n \atop k}\right]=|s(n,k)|=(-1)^{n-k} s(n,k)

بنابراین می‌توان نوشت:

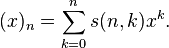
(x)_{n} = \sum_{k=0}^n s(n,k) x^k.

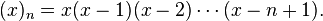
(x)_{n}=x(x-1)(x-2)\cdots(x-n+1).

عدد استرلینگ نوع دوم

عدد استرلینگ نوع دوم را این گونه نمایش می دهیم:

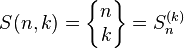
S(n,k)=\left\{\begin{matrix} n \\ k \end{matrix}\right\}= S_n^{(k)}


عدد استرلینگ نوع دوم را با استفاده از نمادگذاری بالا چنین تعریف می‌کنیم:

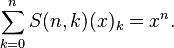
\sum_{k=0}^n S(n,k)(x)_k=x^n.

همچنین با استفاده از اعداد بل می‌توان رابطه‌ی زیر را نوشت:

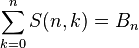
\sum_{k=0}^n S(n,k) = B_n

که  B_n nامین عدد بل است.

 

منبع : ویکی پدیای فارسی

 
  • hossein heydari

نظرات  (۰)

هیچ نظری هنوز ثبت نشده است

ارسال نظر

ارسال نظر آزاد است، اما اگر قبلا در بیان ثبت نام کرده اید می توانید ابتدا وارد شوید.
شما میتوانید از این تگهای html استفاده کنید:
<b> یا <strong>، <em> یا <i>، <u>، <strike> یا <s>، <sup>، <sub>، <blockquote>، <code>، <pre>، <hr>، <br>، <p>، <a href="" title="">، <span style="">، <div align="">
تجدید کد امنیتی