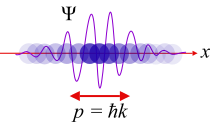
معادله شرودینگر :: وبلاگ علمی دنفر

معادله شرودینگر

دوشنبه, ۷ دی ۱۳۹۴، ۰۱:۴۳ ب.ظ

معادله شرودینگر، معادله‌ای است که چگونگی تغییر حالت کوانتومی یک سامانه فیزیکی با زمان را توصیف می‌کند. این معادله در اواخر سال ۱۹۲۵ فرمول بندی شد و در سال ۱۹۲۶ توسط فیزیکدان اتریشی آروین شرودینگر منتشر گردید.

در مکانیک کلاسیک، معادله حرکت، قانون دوم نیوتن است و فرمولبندی‌های معادل آن، معادله اویلر-لاگرانژ و معادله هامیلتون هستند. در همه این فرمول بندی‌ها، برای حل حرکت یک سیستم مکانیکی و پیشگویی ریاضی اینکه سامانه در هر زمان پس از شرایط و پیکربندی‌های اولیه چه حالتی خواهد داشت، استفاده می‌شوند. در مکانیک کوانتومی مشابه قانون دوم نیوتن، معادله شرودینگر برای یک سامانه کوانتومی (معمولاً اتم‌ها، مولکولها، ذرات ریز اتمی (آزاد، بسته، موضعی)) است. این معادله یک معادله جبری ساده نیست ولی (عموماً) یک معادله دیفرانسیل جزئی خطی است. معادله دیفرانسیل شامل تابع موج برای سیستم است که حالت کوانتومی یا بردار حالت نیز نامیده می‌شود.

در تفسیر استاندارد از مکانیک کوانتومی، تابع موج کاملترین توضیحی است که می‌توان در مورد یک سامانه فیزیکی داد. راه حل‌های معادله شرودینگر نه تنها سامانه‌های مولکولی، اتمی و ریز اتمی را توصیف می‌کند بلکه سیستم‌های ماکروسکوپی، حتی کل جهان را نیز توصیف می‌کند. همانند قانون دوم نیوتن، معادله شرودینگر از لحاظ ریاضی می‌تواند به فرمولبندی‌های دیگر از جمله مکانیک ماتریسی ورنر هایزنبرگ و فرمولبندی انتگرال سطحی زیمان تبدیل شود. همچنین همانند قانون دوم نیوتون، معادله شرودینگر زمان را به طریقی توصیف می‌کند که برای نظریه‌های نسبیتی مناسب نیست. مشکلی که در مکانیک ماتریسی به اندازه کافی شدید نیست و در فرمولبندی انتگرال سطحی به طور کامل حضور ندارد.

معادله

۱٫۱-معادله وابسته به زمان

شکل معادله شرودینگر به شرایط فیزیکی بستگی دارد (پایین را برای موارد خاص مشاهده کنید). عمومی‌ترین شکل آن معادله شرودینگری است که تحول زمانی سیستم را نشان می‌دهد:

معادله وابسته به زمان شرودینگر (عمومی) (کُلی)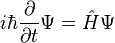

$i \hbar \frac{\partial}{\partial t}\Psi = \hat H \Psi$

که Ψ تابع موج سیستم کوانتومی، i واحد موهومی، ħ ثابت کاهیده پلانک و $\hat{H}$ عملگر هامیلتونی است که انرژی کل به ازای هر تابع موج داده شده را مشخص می‌کند و شکل‌های مختلفی را بسته به شرایط، به خود می‌گیرد. معروفترین نمونه آن معادله غیر نسبیتی شرودینگر برای ذره‌ای که در میدان الکتریکی در حال حرکت است، می‌باشد (نه در میدان مغناطیسی).

معادله وابسته به زمان شرودینگر (عمومی) (برای تک ذره؛ غیرنسبیتی)

$i\hbar\frac{\partial}{\partial t} \Psi(\mathbf{r},t) = \left [ \frac{-\hbar^2}{2m}\nabla^2 + V(\mathbf{r},t)\right ] \Psi(\mathbf{r},t)$

که m جرم ذره، V انرژی پتانسیل آن، ²∇ لاپلاسین و Ψتابع موج است (که با دقت بیشتر، در این متن، تابع موج فضا مکان نامیده می‌شود). به عبارت دیگر این معادله می‌تواند اینگونه توصیف شود: «انرژی کل برابر است با انرژی جنبشی بعلاوه انرژی پتانسیل»، اما کلمات شکل نا مأنوسی به دلایلی که در زیر شرح داده شده‌اند به خود می‌گیرند. با توجه به عملگرهای دیفرانسیلی خاص درگیر، این معادله، یک معادله دیفرانسیل جزئی خطی است و همان‌طور که از اسمش بر می‌آید معادله موج است. لفظ «معادله شرودینگر» به هر دو، معادله عمومی (اولین جعبه بالا) یا نوع خاص غیر نسبیتی آن (دومین جعبه بالا) اشاره می‌کند. معادله عمومی به طور واقعی کاملاً عمومی است، که به وسیله مکانیک کوانتومی و برای همه چیز از معادله دیراک گرفته تا برای نظریه کوانتومی به وسیله تبدیل شدن به عبارات پیچیده مختلف برای هامیلتونی، استفاده می‌شود. نوع خاص غیر نسبیتی شکل ساده شده نزدیک به واقعیت است که در شرایط بسیاری دقیق است و در موارد اندکی دقیق نیست. (مکانیک کوانتومی را ببینید) برای به دست آوردن معادله شرودینگر، عملگر هامیلتونی برای سیستم جهت محاسبه انرژی پتانسیل و انرژی جنبشی ذرات تشکیل دهنده سیستم و جایگذاری در معادله شرودینگر تنظیم شده است. معادله دیفرانسیل جزئی بدست آمده برای تابع موج حل می‌شود که شامل اطلاعاتی درباره سیستم است.

معادله مستقل از زمان

معادله مستقل از زمان شرودینگر پیش بینی می‌کند که توابع موج می‌توانند امواج ایستاده تشکیل دهند که حالتهای ثابت نامیده می‌شوند. (همچنین به عنوان اربیتال در اربیتالهای اتمی یا مولکولی نامیده می‌شوند) این حالت‌ها به نوبهٔ خود مهم هستند. علاوه بر این اگر این حالت‌های پایا دسته‌بندی و تفهیم شوند، حل معادله مستقل از زمان شرودینگر برای هر حالت آسان تر می‌شود. معادله مستقل از زمان شرودینگر حالت‌های پایا را توصیف می‌کند. (این معادله فقط زمانی استفاده می‌شود که خود هامیلتونی وابسته به زمان نیست)

معادله مستقل از زمان شرودینگر (عمومی)

$E\Psi=\hat H \Psi$

به بیان دیگر، در این معادله وقتی که عملگر هامیلتونی به روی تابع موج ''Ψ'' عمل می‌کند، نتیجه ممکن است با همان تابع موج ''Ψ'' متناسب باشد. اگر اینگونه باشد، ''Ψ'' یک حالت پایا است و ثابت تناسب، E انرژی آن حالت ''Ψ'' است. معادله مستقل از زمان شرودینگر به تفصیل در زیر بحث شده است. در واژگان جبر خطی این معادله، یک معادله ویژه مقداری است.

همانند قبل، مشهورترین شکل معادله غیر نسبیتی شرودینگر برای یک ذره مفرد متحرک در میدان الکتریکی (نه مغناطیسی) است.

معادله مستقل از زمان شرودینگر (یک ذره غیر نسبیتی)

$E \Psi(\mathbf{r}) = \left[ \frac{-\hbar^2}{2m}\nabla^2 + V(\mathbf{r}) \right] \Psi(\mathbf{r})$

تعاریف همانند بالا هستند.

مفاهیم

معادله شرودینگر و روش‌های آن شامل یک موفقیت در تفکر فیزیک شد. این معادله در نوع خود اولین بود و راه حل‌های آن منجر به خاصیت‌های غیر معمول و غیر منتظره‌ای برای زمان شد.

انرژی کل، جنبشی و پتانسیل

شکل کلی معادله، غیر معمول و غیر منتظره نیست، معادله شرودینگر می‌تواند به عنوان (انرژی پتانسیل + انرژی جنبشی = انرژی کل) تفسیر شود. این رابطه دقیقاً مانند فیزیک کلاسیک است. به عنوان مثال یک ترن هوایی بدون اصطکاک انرژی کل ثابتی دارد، بنابراین هنگامی که در ارتفاع بالا قرار دارد (انرژی پتانسیل بالا)، آهسته‌تر حرکت می‌کند (انرژی جنبشی کم) و بر عکس.

کوانتش

معادله شرودینگر پیشبینی می‌کند اگر خواص مشخصی از سیستم اندازه‌گیری شوند، نتیجه ممکن است کوانتیده باشد به این معنی که تنها مقادیر گسسته خاصی می‌تواند امکان بیافتد. یک مثال از کوانتش انرژی است: انرژی یک الکترون در یک اتم همواره یکی از ترازهای انرژی کوانتیده است، حقیقتی که توسط طیف اتمی کشف شد. (کوانتش انرژی در زیر بحث شده است) مثال دیگری از کوانتش تکانه زاویه‌ای است. این یک فرض در مدل اولیه اتم بور بود ولی در حقیقت پیشگویی معادله شرودینگر است. همهٔ اندازه‌گیری‌ها نتیجه کوانتیده در مکانیک کوانتومی ندارند. به عنوان مثال مکان، تکانه، زمان و انرژی (گاهی اوقات) می‌توانند هر مقداری در یک بازهٔ پیوسته داشته باشند.

اندازه‌گیری و عدم قطعیت[ویرایش]

در مکانیک کلاسیک، هر ذره در هر لحظه، یک تکانه و مکان دقیق دارد. این مقادیر به طور دقیق هنگامی که ذره با توجه به قوانین نیوتن حرکت می‌کند، تغییر می‌کند. در کوانتوم مکانیک، ذرات ویژگی‌های مشخصی به طور دقیق ندارند و زمانی که انداره گیری می‌شوند نتیجه از یک توزیع احتمال پیروی می‌کند. معادله شرودینگر توزیع احتمالاتی که هستند را پیشگوئی می‌کند، اما اساساً نمی‌تواند نتایج را به طور دقیق، برای هر اندازه‌گیری پیشگوئی کند. اصل عدم قطعیت هایزنبرگ یک نمونهٔ بارزی از عدم قطعیت در مکانیک کوانتوم است. این اصل بیان می‌کند که هر قدر که مکان ذره با دقت بیشتری مشخص باشد، تکانه را با دقت کمتری خواهیم دانست و بر عکس. معادله موج شرودینگر تکامل تابع موج یک ذره را توصیف می‌کند. حتی اگر تابع موج دقیقاً شناخته شده باشد، نتیجه یک اندازه‌گیری خاص روی آن نادقیق خواهد بود.

تونل زنی کوانتومی

در فیزیک کلاسیک، هنگامی که یک توپ به آرامی به سمت یک تپه می‌غلتد، انتظار می‌رود که توقف کند و بازگردد، زیرا انرژی کافی برای برای عبور به آن طرف ندارد. با این حال معادله شرودینگر پیشگوئی می‌کند که احتمال کمی برای اینکه توپ به آن سوی تپه برود وجود دارد حتی اگر انرژی کمی برای رسیدن به قله داشته باشد؛ که این تونل زنی کوانتومی نامیده می‌شود. تونل زنی کوانتومی به اصل عدم قطعیت ارتباط دارد: اگر چه توپ به نظر می‌رسد که در یک طرف تپه باشد، مکان آن نامشخص است بنابراین شانس این که توپ در طرف دیگر باشد، وجود دارد.

ذرات به عنوان موج

معادله دیفرانسیل غیر نسبیتی شرودینگر نوعی معادله دیفرانسل جزئی است که معادله موج نامیده می‌شود؛ بنابراین ذرات رفتاری که معمولاً به امواج نسبت داده می‌شوند، از خود نشان می‌دهند. یک مثال مشخص از رفتار غیر معمول ذرات که معمولاً امواج از خود نشان می‌دهند، پراش دو شکاف است که به طور مستقیم همراه با ذرات نیست، تداخل امواج از دو شکاف در بعضی از نقاط یکدیگر را خنثی و در برخی نقاط تقویت می‌کنند که باعث به وجود آمدن طرح پراش می‌شود. به طور مستقیم این انتظار را نداریم که این طرح از یک ذره پرتاب شده مشاهده شود، زیرا ذره باید از یکی از دو شکاف عبور کند نه از هر دو شکاف؛ بنابراین چون معادله شرودینگر یک معادله موج است، ذره پرتاب شده دقیقاً همین طرح را نشان می‌دهد. (آزمایش باید به دفعات زیادی انجام شود تا طرح پراش مشاهده شود) ظاهر طرح اثبات می‌کند که الکترون از هر دو شکاف به طور همزمان عبور می‌کند. اگر چه عجیب به نظر می‌رسد، اما این پیشگوئی صحیح است. به طور ویژه، پراش الکترون و نوترون به خوبی تفهیم شده و به صورت گسترده در علوم و مهندسی استفاده می‌شوند. ذرات همچنین برهم نهی و تداخل از خود نشان می‌دهند که با پراش ارتباط دارد. خاصیت برهم نهی به ذرات اجازه می‌دهد که در یک برهم نهی کوانتومی در حالت‌های متفاوت چند گانه در یک زمان باشد، به عنوان مثال یک ذره می‌تواند چندین انرژی مختلف در یک زمان معین داشته باشد و می‌تواند در چندین حالت مختلف در یک زمان باشد. در مثال بالا یک ذره می‌تواند از میان دو شکاف در یک زمان عبور کند.

تفسیر تابع موج[ویرایش]

معادله شرودینگر راهی برای بدست آوردن تابع موج محتمل از یک سیستم و چگونگی تفسیر پویای آن با زمان فراهم می‌کند. اگر چه معادله شرودینگر مستقیماً نمی‌گوید که تابع موج دقیقاً چیست. تفسیر مکانیک کوانتومی سوالاتی مانند اینکه چه رابطه‌ای میان تابع موج هست که اساس واقعی دارد و حاصل اندازه‌گیری‌های تجربی است، را مشخص می‌کند. یک جنبه مهم رابطهٔ میان معادله شرودینگر و فروریزش تابع موج است. در گذشته کپنهاگ می‌گفت: ذرات از معادله شرودینگر پیروی می‌کنند به جز در طول فروریزش تابع موج که در آن مقطع به طور کاملاً متفاوتی رفتار می‌کند. ظهور نظریه کوانتومی decoherance اجازه داد تا روش‌های جایگزین در جایی که معادلهٔ شرودینگر اغنا می‌شود، فروریزش تابع موج باید از نتیجه معادله شرودینگر توضیح داده شود.

معادله موج برای ذرات

معادله شرودینگر بر اساس فرضیه دوبروی توسعه یافت و معادلهٔ بیانگر ذرات که می‌توانست در این راه تولید شود بود برای استخراج بیشتر در حالت ریاضی معادله شرودینگر می‌توانید این را هم ببینید.

فرضیات

پایستگی انرژی: انرژی کل ذرات متشکل از جمع انرژی جنبشی و انرژی پتانسیل است. این جمع معادل هامیلتونی در مکانیک کلاسیک است:

$E = T + V =H \,\!$

در حقیقت برای ذرات در یک بعد با موقعیت مکان x جرم m و تکانه P و انرژی پتانسیل V عموماً با موقعیت زمان t تغییر می‌کند

$E = \frac{p^2}{2m}+V(x,t)=H$

برای سه بعدی‌ها بردار مکان r و بردار تکانهٔ P باید استفاده شود.

$E = \frac{\bold{p}\cdot\bold{p}}{2m}+V(\bold{r},t)=H$

این معادله می‌تواند برای هر تعداد ذره ثابت گسترش یابد: انرژی کل، پس حاصل جمع انرژی‌های جنبشی کل، به علاوه انرژی پتانسیل است؛ که همام هامیلتونی می‌باشد. اگرچه هامیلتونی می‌تواند فعل و انفعالات میان ذرات (یک مسئله چند ذره‌ای) باشد؛ بنابراین انرژی پتانسیل V می‌تواند در پیکر بندی فضایی ذرات و احتمالاً تغییر زمان، تغییر کند انرژی پتانسیل در کل از مجموع انرژی پتانسیل برای هر ذره تشکیل نشده است. این یک تابع برای موقعیت فضایی هر ذره است در واقع:

$E=\sum_{n=1}^N \frac{\bold{p}_n\cdot\bold{p}_n}{2m_n} + V(\bold{r}_1,\bold{r}_2\cdots\bold{r}_N,t) = H \,\!$

روابط دوبروی

فرضیه کوانتوم نور انیشتین (۱۹۰۵) بیانگر این است که انرژی E یک فوتون متناسب است با بسامد ν (یا بسامد زاویه‌ای ω = ۲πν) که به بسته‌های موج کوانتومی نور، مربوط می‌شود

$E = h\nu = \hbar \omega \,\!$

همانند فرضیه دوبروی (۱۹۲۴) بیانگر این است که هر ذره می‌تواند با یک موج و تکانه P ذره از طریق رابطه زیر ارتباط داشته باشد با طول (λ) یک موج کذایی در یک بعد:

، $p = \frac{h}{\lambda} = \hbar k\;$

در سه بعد:

$\mathbf{p} = \frac{h}{\lambda} = \hbar \mathbf{k}\;$

که k بردار موج است (و طول موج با اندازهٔ k ارتباط دارد)

روشی برای معادله

معادله شرودینگر یک معادله موج ریاضی است که بر اساس حرکت‌های موج پاسخ داده شده است. در حالت عادی معادله موج در فیزیک می‌تواند از قوانین دیگر فیزیکی، مشتق گیری شود. معادله موج می‌تواند مشتقی از قوانین دیگر فیزیک باشد و برای ارتعاشات مکانیکی بروی طناب در ماده از قانون نیوتون مشتق شود. تابع موج آنالوگ نشان دهندهٔ جابه جایی ماده است و امواج الکترومغناطیسی از معادلات ماکسول بدست می‌آید که در آن تابع موج در زمینه‌های الکتریکی و مغناطیسی می‌باشد، در مقابل آن، معادلات شرودینگر بر اساس انرژی مواد و قیاس منطقی جداگانه در مکانیک کوانتومی است. دوگانگی ذره-موج از معادلات شرودینگر پیروی می‌کند که در زیر بیان شده است: رابطه پلانک – انیشتین و دوبروی:

$E=\hbar\omega, \quad \bold{p}=\hbar\bold{k}$

رابطه‌ای میان فضا با تکانه، انرژی با زمان را مشخص می‌کند؛ که اگر در معادلات بالا ħ = ۱ معادلات زیر بدست می‌آید:

$E=\omega, \quad \bold{p}=\bold{k}$

انرژی و بسامد زاویه‌ای هر دو یک بعد دارند که با زمان رابطه مستقیمی دارند، تکانه و ععد موج هر دو با طول موج رابطه عکسی دارند. در اواخر ۱۹۲۵ نظریهٔ شرودینگر بیانگر این بود که فاز امواج تخت، مانند فاکتور فازی پیچیده در این روابط استفاده می‌شود.

$\Psi = Ae^{i(\bold{k}\cdot\bold{r}-\omega t)} = Ae^{i(\bold{p}\cdot\bold{r}-Et)/\hbar}$

و برای دانستن مشتقات جزئی مرتبه اول نسبت به مکان:

$\nabla\Psi = \dfrac{i}{\hbar}\bold{p}Ae^{i(\bold{p}\cdot\bold{r}-Et)/\hbar} = \dfrac{i}{\hbar}\bold{p}\Psi$

و زمان:

$\dfrac{\partial \Psi}{\partial t} = -\dfrac{i E}{\hbar} Ae^{i(\bold{p}\cdot\bold{r}-Et)/\hbar} = -\dfrac{i E}{\hbar} \Psi$

حاکی از مشتقات

$\begin{matrix} -i\hbar\nabla\Psi = \bold{p}\Psi & \rightarrow & -\dfrac{\hbar^2}{2m}\nabla^2\Psi = \dfrac{1}{2m}\bold{p}\cdot\bold{p}\Psi \\ \dfrac{\partial \Psi}{\partial t} = -\dfrac{i E}{\hbar} \Psi & \rightarrow & i\hbar\dfrac{\partial \Psi}{\partial t} = E \Psi \\ \end{matrix}$

با ضرب Ψ در معادله انرژی

$E= \dfrac{\bold{p}\cdot\bold{p}}{2m}+V \rightarrow E\Psi= \dfrac{\bold{p}\cdot\bold{p}}{2m}\Psi+V\Psi$

بلافاصله معادله شرودینگر به دست می‌آید:

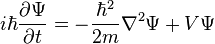
$i\hbar\dfrac{\partial \Psi}{\partial t}= -\dfrac{\hbar^2}{2m}\nabla^2\Psi +V\Psi$

قیاس منطقی دیگر در مکانیک کوانتومی این است که همه مشاهده گرها توسط عملگرهایی که روی تابع موج عمل می‌کنند، نشان داده می‌شوند. ویژه مقادیر عملگرها مقادیری هستند که مشاهده گرها به خود می‌گیرند. مشتقات قبلی بر اساس مشتقات زمان به عملگرهای انرژی ختم می‌شوند.

$\hat{E}= i\hbar\dfrac{\partial}{\partial t}$

و عملگر تکانه بر اساس مشتقات فضایی: $\bold{\hat{p}}= -i\hbar\nabla$ می‌باشد. این‌ها عملگرهای دیفرانسیلی هستند، که به جز انرژی پتانسیل V که فقط یک فاکتور ضربی است. جایگذاری این عملگرها در معادله انرژی توسط Ψ به همان معادله موج بر می‌گردد؛ و نکته جالب این است که انرژی و تکانه یک تقارن با زمان دارد و اینها دلایلی هستند که در آن انرژی و تکانه پایسته می‌مانند. انرژی جنبشی Tبا مربع تکانه pرابطه دارد. وقتی تکانه ذره، افزایش می‌یابد انرژی جنبشی به سرعت افرایش پیدا می‌کند. اما وقتی عدد موج k افزایش پیدا می‌کند طول موج $\scriptstyle \lambda$ کاهش می‌یابد

$\bold{p}\cdot\bold{p} \propto \bold{k}\cdot\bold{k} \propto T \propto |\nabla^2\Psi| \propto \dfrac{1}{\lambda^2}$

جواب برای معادله

جواب عمومی معادله می‌تواند به راحتی در قسمت پایین دیده شود. امواج تخت قطعاً یک جواب است چون برای بدست آوردن تابع استفاده شده است. همچنین هر ترکیب خطی از امواج ساده یک جواب است. برای هر k‌های گسسته، هر ترکیب خطی، یک برهم نهی امواج تخت است

$\Psi(\bold{r},t) = \sum_{n=1}^\infty A_n e^{i(\bold{k}_n\cdot\bold{r}-\omega_n t)} \,\!$

و برای k‌های پیوسته هر ترکیب خطی، یک انتگرال است که بسط فوریهٔ تکانهٔ فضایی تابع موج است

$\Psi(\bold{r},t) = \frac{1}{(\sqrt{2\pi})^3}\int\Phi(\bold{k})e^{i(\bold{k}\cdot\bold{r}-\omega t)}d^3\bold{k} \,\!$

که d³k = dk_xdk_ydk_z می‌باشد؛ که انتگرال به روی فضای k گرفته می‌شود و تابع موج در فضای تکانه (Φ(k از زیر انتگرال به دست می‌آید. از آنجایی که اینها معادله شرودینگر را اغنا می‌کند، جواب معادله شرودینگر برای شرایط داده شده فقط برای بدست آوردن امواج تخت، استفاده نمی‌شود، بلکه هر تابع موجی که معادله شرودینگر، به دست آمده از سیستم، علاوه بر شرایط مرزی مربوط، را اغنا کند، استفاده می‌شود. می‌توان نتیجه گرفت معادله شرودینگر برای شرایطی (غیر نسبیتی) درست است.

موج و حرکت ذره

شرودینگر فرض نکرد که جواب بسته موج (نه فقط برای امواج تخت) در مکان r و عدد موج k در طول یک مسیر مشخص شده، توسط مکانیک کلاسیک، در حدی که طول موج کوتاه است $\scriptstyle \lambda \,\!$ حرکت خواهد کرد. برای مثال، برای یک k بزرگ و در نتیجه P بزرگ در مقایسه با ثابت کاهیده پلانک ħ. به عبارت دیگر در حدی که ħ به صفر میل میل می‌کند، معادلات مکانیک کلاسیک از معادلات مکانیک کوانتومی، به دست می‌آیند. حاصل استفاده از اصل عدم قطعیت هایزنبرگ برای مکان و تکانه صفر می‌شود و این مانند این است که ثابت کاهیده پلانک به صفر میل کند ħ → ۰.

$\sigma(x) \sigma(p_x) \geqslant \frac{\hbar}{2} \quad \rightarrow \quad \sigma(x) \sigma(p_x) \geqslant 0 \,\!$

که σ بیانگر عدم قطعیت اندازه‌گیری در x و p_x (و شبیه به آن در مسیرهای y و z) است؛ که بیان می‌کند که مکان و تکانه در این حد، می‌توانند با دقت دلخواه مشخص شوند.

که این فرم عمومی معادله شرودینگر به صورت زیر است:

$i\hbar \frac{\partial}{\partial t} \Psi\left(\mathbf{r},t\right) = \hat{H} \Psi\left(\mathbf{r},t\right) \,\!$

که با معادله هامیلتون-ژاکوبی رابطهٔ نزدیکی دارد:

$\frac{\partial}{\partial t} S(q_i,t) = H\left(q_i,\frac{\partial S}{\partial q_i},t \right) \,\!$

جایی که S کنش است وH تابع هامیلتونی است (نه عملگر). تعمیم مختصات، q_i برای i = ۱٬۲٬۳ می‌تواند موقعیت در مختصات دکارتی را، هماهنگ کند.

با جایگذاری ، $\Psi = \sqrt{\rho(\mathbf{r},t)} e^{iS(\mathbf{r},t)/\hbar}\,\!$ که ρ چگالی احتمال است سپس اگر از معادله بدست آمده حد ħ → ۰ گرفته شود معادله هامیلتونی-ژاکوبی بدست خواهد آمد.

حرکت یک ذره توسط (طول موج کوتاه) جواب بسته موج، برای معادله موج شرودینگر توضیح داده شده است که همچنین توسط معادله ژاکوبی-هامیلتونی نیز بیان شده است.
معادله شرودینگر شامل تابع موج است، بنابراین جواب بسته موج موقعیت ذره (کوانتومی) که به صورت نا منظم در جبهه موج قرار دارد، را بیان می‌کند. در مقابل، معادله ژاکوبی-هامیلتونی بیان می‌کند که یک ذره (کلاسیکی) مکان و تکانه به طور همزمان می‌توانند مشخص باشند.

مستقل از زمان

اگر هامیلتونی تابعی صریح از زمان نباشد معادله به بخش‌های زمانی و مکانی قابل تفکیک است. عملگر انرژی $\hat{E} = i \hbar \partial / \partial t \,\!$ می‌تواند توسط مقادیر ویژه انرژی جایگزین شود؛ که فرم خلاصه شده معادله ویژه مقداری برای هامیلتونی $\hat{H}$ است.

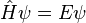
$\hat H \psi = E \psi$

یک جواب معادله مستقل از زمان، یک ویژه حالت انرژی E نامیده می‌شود. برای پیدا کردن حالت وابستگی زمانی از معادله وابسته به زمان با شرایط اولیهٔ (ψ(r شروع می‌کنیم. مشتق زمانی در t = ۰متناسب است با

$\left.i\hbar \frac{\partial}{\partial t} \Psi(\bold{r},t)\right|_{t=0}= \left.H \Psi(\bold{r},t)\right|_{t=0} =E \Psi(\bold{r},0) \,$

بنابراین معادله را به دو بخش زمانی و مکانی تفکیک کرده و معادله کلی حاصلضرب این دو است پس برای هر زمان t:

$\Psi(\bold{r},t)= \tau(t) \psi(\bold{r}) \,$

اکنون Ψ را جایگذاری می‌کنیم:

$i\hbar \frac{\partial \Psi}{\partial t } = E \Psi \rightarrow i\hbar \psi(\bold{r})\frac{\partial\tau(t)}{\partial t } = E \tau(t)\psi(\bold{r}) \,$

که در این حالت (ψ(r حذف شده معادله برای $\scriptstyle \tau(t)\,\!$ حل می‌شود که یک جواب معادلهٔ وابسته به زمان را با شرایط اولیه بیان می‌کند.

$\Psi(\bold{r},t) = \psi(\bold{r}) e^{-i{E t/\hbar}} = \psi(\bold{r}) e^{-i{\omega t}} \,$

این موضوع جواب معادله وابسته به زمان امواج ایستاده را بیان می‌کند که حالتی با انرژی مشخص است. (که به جای توزیع احتمالاتی برای انرژِی‌های متفاوت) در فیزیک این امواج ایستاده حالت پایا یا ویژه حالت انرژی نامیده می‌شود. ویژه مقادیر انرژی از این معادله یک طیف مجزا دارد؛ بنابراین انرژی باید کوانتیده باشد. به طور خاص ویژه حالت انرژی یک پایه - هر تابع موج ممکن است به صورت جمع حالت‌های انرژی مجزا یا انتگرال حالت‌های انرژی پیوسته نوشته شود این نظریه طیف در ریاضیات نامیده می‌شود.

مکانین کوانتوم
دو گانگی موج و ذره

۰ ۰
۹۴/۱۰/۰۷

hossein heydari

وبلاگ علمی دنفر

وبلاگ علمی دنفر

ریاضیات و فیزیک ، جهانی جدا

وارد علـم شو ، تا از مـا شوی !

مقالات علمی

دانشمندان

ریاضیات

شخصیت ها

اخبار علمی

پزشکی

نظریه ها ( تئوری ها )

کانگورو

اثبات ها

شفق قطبی

ویدئو ها

فیزیک

سخن بزرگان

جبر

هندسه

سفینه های فضایی

سفرات فضایی

الکتریسیته و مغناطیس

سیارات

انرژی هسته ای

جان نش