اتحاد های جبری
در ریاضیات اتحادها تساوی هایی هستند که به ازای هر مقدار عددی از دامنه خود که بجای متغییرهایشان قرار دهیم همواره برقرار باشند. به عنوان مثال تساوی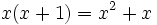 برای هر x عضو دامنه برقرار است. لذا این عبارت جبری یک اتحاد است، اما تساوی
برای هر x عضو دامنه برقرار است. لذا این عبارت جبری یک اتحاد است، اما تساوی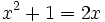 فقط برای x=1 برقرار است. پس این عبارت یک اتحاد نمی باشد. در واقع در مورد یک اتحاد در اصل به یک تساوی بدیهی چون 0=0 می رسیم.
فقط برای x=1 برقرار است. پس این عبارت یک اتحاد نمی باشد. در واقع در مورد یک اتحاد در اصل به یک تساوی بدیهی چون 0=0 می رسیم.
به عنوان مثال در اتحاد مثال زده شده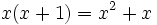 دو طرف ساده شده و تساوی 0=0 حاصل می شود.
دو طرف ساده شده و تساوی 0=0 حاصل می شود.
به این ترتیب تفاوت میان یک اتحاد جبری و یک معادله جبری در این است که اتحاد جبری به ازای همه مقادیر دامنه برقرار است در صورتی که یک معادله جبری به ازای تعداد محدودی از اعضای دامنه(مجموعه جواب معادله) برقرار است.
عبارات زیر نمونه ای از اتحاد است:
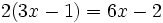
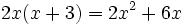
اتحادهای مهم جبری
در میان اتحادهای جبری، برخی از اتحادها بسیار مهم و کاربردی می باشند و در حل معادلات، محاسبات جبری، تجزیه عبارت جبری و... بسیار کاربرد دارند. از این رو دانستن و به کاربردن آنها از اهمیت خاصی برخوردار است. در این قسمت به بررسی این اتحادهای مهم می پردازیم.
اتحاد مربع مجموع دو جمله
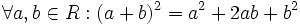
اتحاد مربع تفاضل دو جمله

اتحاد مکعب مجموع دو جمله
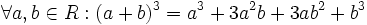
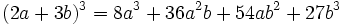
اتحاد بسط دو جمله ای نیوتن
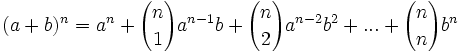
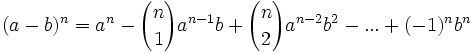
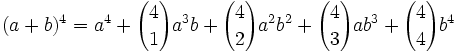

اتحاد مربع سه جمله
تعمیم اتحاد مربع چند جمله
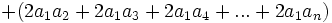
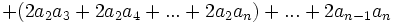

اتحاد مزدوج
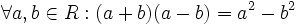
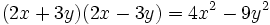
- لازم به توضیح است اگر داشته باشیم a+b آنگاه عبارت a-b را مزدوج عبارت اول یعنی a+b می گویند.
اتحاد جمله مشترک
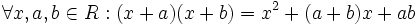
تعمیم اتحاد جمله مشترک
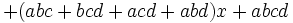
- این روال به همین ترتیب برای حالات دیگر هم برقرار است.
مثال:
اتحاد مجموع مکعبات دو جمله(اتحاد چاق و لاغر)
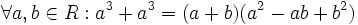
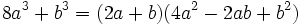
تعمیم اتحاد مجموع مکعبات دو جمله(اتحاد چاق و لاغر)
پس می توان نتیجه زیر را بیان کرد:

- لازم به توضیح است که این اتحاد فقط برای حالتی برقرار ست که توان n عدد طبیعی فرد باشد.
مثال:
اتحاد تفاضل مکعبات دو جمله(اتحاد چاق و لاغر)

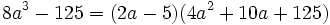
تعمیم اتحاد تفاضل مکعبات دو جمله(اتحاد چاق و لاغر)
پس می توان نتیجه زیر را بیان کرد:

- لازم به توضیح است این این اتحاد برای هر عدد طبیعی n برقرار است.
مثال:
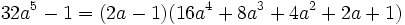
اتحاد اویلر
- برهان:
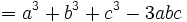
- صورتی دیگر از اتحاد اویلر:
- برهان:
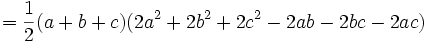
-
نتایج اتحاد اویلر:
- اگر a+b+c=0 آنگاه
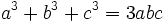
- اگر a=b=c آنگاه
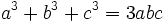
مثال:
همچنین اگر 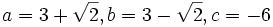 باشد آنگاه داریم:
باشد آنگاه داریم:
اتحاد لاگرانژ
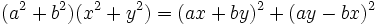
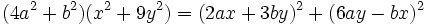
- ۹۴/۰۹/۲۷

