انتگرال

 

نمایش گرافیکی انتگرال.

اَنتِگرال (به انگلیسی: Integral) مقدار مشترک ممکن زیرینۀ مجموعه‌ای ریمانی و زبرینۀ مجموعه‌ای ریمانی یک تابع حقیقی در بازۀ مفروض است.^[۱] انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل می‌دهند.

نخستین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد.

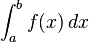
 و  نقاط ابتدا و انتهای بازه هستند و  تابعی انتگرال‌پذیر است و 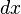 نمادی برای متغیر انتگرال‌گیری است.

از لحاظ تاریخی 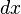 یک کمیت بی‌نهایت کوچک را نشان می‌دهد. هر چند در تئوری‌های جدید، انتگرال‌گیری بر پایه متفاوتی پایه‌گذاری شده‌است.

هندسه ی اقلیدسی

 

اقلیدس ریاضیدان یونانی،پسر نوقطرس بن برنیقس،ریاضیدان و منجم بزرگ تاریخ علم،به سال 323 ق.م متولد شد،وی از تبار فنیقی و نخستین رئیس بخش ریاضیات بود، در زبان یونانی اقلی به معنی کلید و دس به معنای هندسه و اقلیدس به معنای کلید هندسه است،در آن زمان مرگ اسکندر فرا رسید و سردارانش برای کسب قدرت با یکدیگر جنگیدند. بطلمیوس یکی از سرداران اسکندر بود که مصر را گرفت و در آن جا تشکیل حکومت داد. وی از علم و دانش حمایت می کرد و دانشمندان و دوستداران علم و دانش را دعوت می کرد تا در اسکندریه اقامت کنند. 
اقلیدس بیش از 30 سال نداشت که به خواهش و درخواست بطلمیوس برای تدریس به اسکندریه رفت و در این شهر مکتب فلسفی خود را پایه گذاری کرد. اقلیدس مردی محبوب، آرام، فروتن و نیکوکار بود و در حضور مستبدان و سرداران زورگو در نهایت صراحت صحبت می کرد. بطلمیوس فرمانروای مصر هنگامی که خواست هندسه را بیاموزد آن را دشوار دید و ترجیح داد که از راه ساده تری به فهم آن موفق شود، بنابر این از اقلیدس پرسید: آیا امکان دارد قضایا را به نحو ساده تری بیان کرد؟ اقلیدس به وی جواب داد: غیر ممکن است، در هندسه راه مخصوص شاهانه وجود ندارد!